I. Function

Type: RemoteJudge

1000ms

256MiB

You cannot submit for this problem because the contest is ended. You can click "Open in Problem Set" to view this problem in normal mode.

题目描述

有n个连续函数fi(x)，其中1≤i≤n。对于任何两个函数fi(x)和fj(x),(i!=j)，恰好存在一个x使得fi(x)=fj(x)，

并且存在无穷多的x使得fi(x)<fj(x)。对于任何i;j;k，满足1≤i<j<k≤n，则不存在x使得fi(x)=fj(x)=fk(x)。

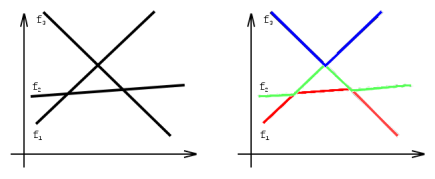
如上左图就是3个满足条件的函数，最左边从下往上依次为f1;f2;f3。右图中红色部分是这整个函数图像的最低层

，我们称它为第一层。同理绿色部分称为第二层，蓝色部分称为第三层。注意到，右图中第一层左边一段属于f1，

中间属于f2，最后属于f3。而第二层左边属于f2，接下来一段属于f1，再接下来一段属于f3，最后属于f2。因此，

我们称第一层分为了三段，第二层分为了四段。同理第三层只分为了两段。求满足前面条件的n个函数，第k层最少

能由多少段组成。

一行两个整数n; k。1 ≤ k ≤ n ≤ 100。

一行一个整数，表示n 个函数第k 层最少能由多少段组成。

1 1